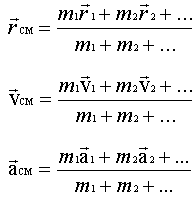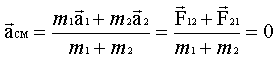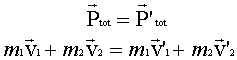| Centre de masse et conservation de la quantité de mouvement - théorie |
|
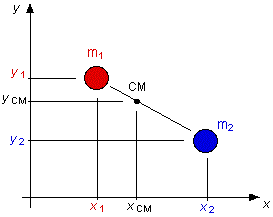
Le centre de masse (CM) La position du centre de masse d'un système composé de deux particules s'obtient en considérant les coordonnées de position x et y de chacune des particules.
|
|
Le principe de la conservation de la quantité de mouvement Lors d'une collision entre deux particules, elles interagissent l'une sur l'autre selon la troisième loi de Newton (elles exercent mutuellement l'une sur l'autre des forces de même grandeur mais de sens opposés). Dans de telles situations, l'accélération du centre de masse est nulle car la somme des forces mutuelles qu'exercent les masses l'une sur l'autre est nulle. Les accélérations des masses sont de sens contraires.
Si l'accélération du centre de masse est nulle, ce dernier conserve donc sa vitesse (grandeur et orientation). Ceci est vrai tant qu'aucune force extérieure résultante est appliquée sur le système. Pour un système composé de deux particules, le principe de conservation de la quantité de mouvement s'exprime alors
La quantité de mouvement totale d'un système n'est pas affectée par les interactions entre les composantes de ce système. La quantité de mouvement totale d'un système est une grandeur vectorielle qui dépend du vecteur vitesse de chacune des composantes du système. La capsule suivante explique, en faisant appel à la notion d'impulsion, comment peut se démontrer le principe de conservation de la quantité de mouvement. Cette autre capsule donne quelques exemples d'application du principe de conservation de la quantité de mouvement.
|
| Les différents types de collisions
C'est la quantité de mouvement totale d'un système qui est conservée lorsque les particules du système interagissent entre elles (le système est soumis à une force extérieure résultante nulle). Dans la plupart des collisions (entre deux véhicules par exemple), l'énergie cinétique totale du système n'est pas conservée. Les différents types de collisions sont définis en fonction du bilan énergétique de la collision (interaction).
Vous pouvez consulter la capsule suivante décrivant le fonctionnement du pendule balistique. |