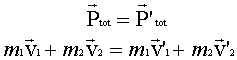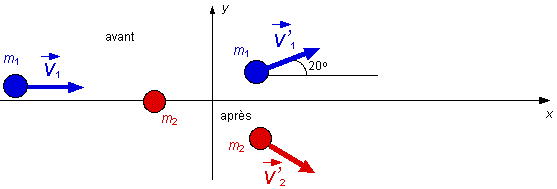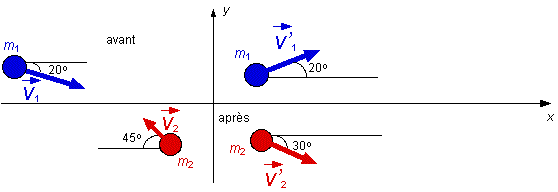Dans les exemples qui suivent, nous appliquerons ce principe.

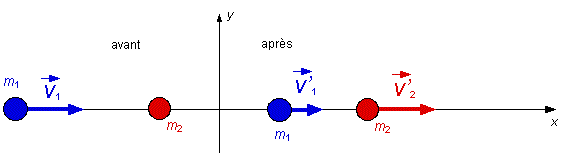
Il est très important de comprendre que la quantité de mouvement d'une particule est une grandeur vectorielle.

Premier cas (collision linéaire sur l'axe x)
Une masse m₁ de 3 kg, ayant une vitesse de 5 m/s selon l'axe x, heurte une masse m₂ de 2 kg initialement immobile. Si la masse m₂ possède, après la collision, une vitesse de 4 m/s, quelle doit être la vitesse de la masse m₁ suite à cette collision ?

Le bilan énergétique de cette collision :
L'énergie cinétique totale avant la collision était de 37,5 J = ½ (m₁ v₁²)
L'énergie cinétique totale après la collision : ½(3)(2,33)² + ½(2)(4)² = 8,17 + 16,0 = 24,2 J

Lors de cette collision, 35,5 % de l'énergie cinétique initiale est perdue. Cette collision est inélastique.

Deuxième cas (collision linéaire parfaitement inélastique sur l'axe x)

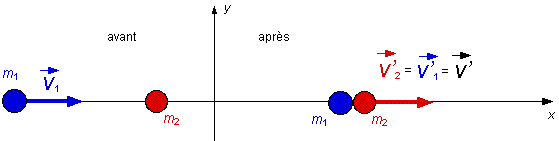
Une collision est dite parfaitement inélastique lorsque les masses en interaction restent liées l'une à l'autre à la suite de cette interaction. C'est dans ce type de collision (ou interaction) que le système perd le maximum d'énergie cinétique. Dans ce deuxième cas, les conditions initiales sont les mêmes que dans le premier. Il faut donc appliquer le principe de conservation de la quantité de mouvement totale du système pour trouver la vitesse commune des deux masses après la collision.

m₁v_1x = (m₁+ m₂)v' = 15 (kg · m)/s

v' = 3,0 m/s

Le bilan énergétique de cette collision :
L'énergie cinétique totale avant la collision était de 37,5 J = ½ (m₁ v₁²)
L'énergie cinétique totale après la collision : ½(3 + 2)(3,0)² = 22,5 J

Lors de cette collision, 40 % de l'énergie cinétique initiale est perdue. Cette collision étant parfaitement inélastique, ce pourcentage représente le maximum que peut perdre ce système.

Troisième cas (collision à deux dimensions)
Dans ce troisième cas, les conditions initiales sont les mêmes que dans les situations précédentes. Comme le centre de masse de m₁ n'est pas sur l'axe x, la collision ne sera pas linéaire. Il faut donc considérer les composantes en x ainsi qu'en y de la quantité de mouvement de chacune des deux masses après la collision.

Si après la collision, la vitesse de m₁ a un module de 4 m/s et que cette vitesse est orientée à 20 degrés par rapport à l'axe x, quelle sera la grandeur ainsi que l'orientation de la vitesse de la masse m₂ après la collision ?

La conservation de la quantité de mouvement totale :

selon x :

m₁v_1x = m₁v'_1x + m₂v'_2x = 15

  m₁v'₁cos20^o + m₂v'₂cosq₂ = 15

m₂v'₂cosq₂ = 15 - 11,3 = 3,72  (1)

selon y :

m₁v'_1y + m₂v'_2y = 0

m₁v'₁sin20^o + m₂v'₂sinq₂ = 0

m₂v'₂sinq₂ = - 4,10   (2)

En divisant l'équation (2) par l'équation (1), on obtient que tanq = - 1,10 ce qui donne q₂ = - 47,8^o (angle conventionnel mesuré sous l'axe x), le module de la vitesse de m₂ après la collision est donc de 2,77 m/s.

Le bilan énergétique de cette collision :
L'énergie cinétique totale avant la collision est toujours de 37,5 J = ½ (m₁ v₁²)
L'énergie cinétique totale après la collision : ½(3)(4)² + ½(2)(2,77)² = 24,0 + 7,67 = 31,7 J

Lors de cette collision, 15,5 % de l'énergie cinétique initiale est perdue. Cette collision est inélastique.

Exercices (collision à deux dimensions) :

Le schéma ci-haut donne l'orientation de chacune des vitesses avant et après une collision se produisant entre deux masses, m₁ = 3 kg et m₂ = 2 kg. 

(a) Si le module de la vitesse de la masse m₁ est de 5 m/s avant la collision, que celui de m₂ est de 1,5 m/s, quelle est la vitesse de chacune des masses après cette collision ?

(b) De quel type de collision s'agit-il ?

Réponses :
(a) v'₁= 1,47 m/s et v'₂ = 4,52 m/s  (b) La collision est inélastique
 car 40,4 % de l'énergie cinétique initiale est perdue.