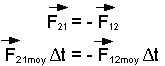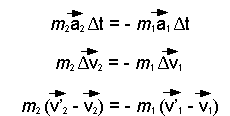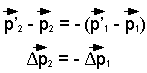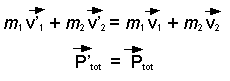Les collisions

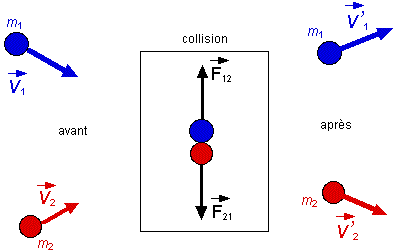
Lors d'une collision entre deux particules, les masses interagissent l'une sur l'autre selon la troisième loi de Newton. Pendant que les masses sont en contact, les forces mutuelles qu'elles exercent l'une sur l'autre sont, à tout instant, de même module et de sens contraires.

Comment les vitesses initiales et finales des masses en interaction sont elles reliées entre elles ? En appliquant la troisième loi de Newton nous pouvons établir que :

(1)

L'impulsion
Le produit FDt s'appelle l'impulsion I. L'impulsion est une grandeur vectorielle ayant la même orientation que la force appliquée. L'expression I = FDt est valable uniquement lorsque la force est constante, si la force est variable, comme c'est généralement le cas lors d'une collision, l'impulsion est donnée par l'aire sous la fonction de force en fonction du temps. Il est possible de déterminer une valeur moyenne pour la force d'interaction entre les particules pendant l'intervalle de temps Dt que dure l'interaction. Cette force moyenne multipliée par Dt correspond à l'aire sous la fonction.

Exemple de la force appliquée sur un corps en fonction du
temps. L'aire sous cette fonction donne l'impulsion reçue.

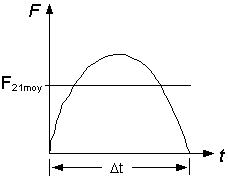
Le vecteur impulsion reçue par chacune des masses est nécessairement de même module mais de sens opposés, que la force soit constante ou pas, en autant que les forces sont le résultat d'une interaction entre deux particules.

Continuons notre démonstration... puisque F = ma (F et a étant des grandeurs vectorielles) remplaçons, dans l'équation (1) plus haut, F par ma où a est l'accélération moyenne de chacune des particules :

(2)

La dernière équation montre que l'impulsion reçue par une particule correspond à sa variation de quantité de mouvement. Nous pouvons écrire l'équation (2) sous la forme suivante :

Ainsi nous obtenons le principe de conservation de la quantité de mouvement totale d'un système.

La capsule suivante donne quelques exemples d'application de ce principe.