Les deux fils placés bout à bout sont en série
et donc parcourus par le même courant

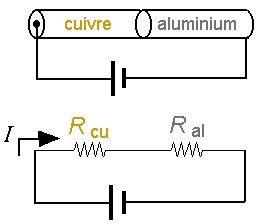
(a) Comme les deux fils sont en série, le rapport des courants est nécessairement 1.

I_cu/I_al = 1

(b) La différence de potentiel aux bornes d'une résistance est donnée par le produit de la résistance par le courant. Comme le courant est le même pour chacune des résistances, Le rapport des différences de potentiel est le même que le rapport des résistances. La résistance d'un conducteur de longueur L, ayant une aire de section transversale A, fabriqué à l'aide d'un matériau de résistivité r est donnée par

R = r L / A

Comme les conducteurs ont la même longueur ainsi que le même diamètre, le rapport entre leur résistances est le même qu'entre leurs résistivités.

DV_cu/DV_al = R_cu/R_al = r_cu/r_al = 0,61

(c) La puissance dissipée par une résistance peut s'exprimer en fonction du courant passant par celle-ci.

P = R I ² 

Comme le courant est le même pour les deux conducteurs, le rapport des puissances dissipées est le même que le rapport des résistances (ou des différences de potentiel).

P_cu/P_al = 0,61

(d) En considérant uniforme le champ électrique à l'intérieur de chaque conducteur, le module du champ est donné par l'équation

E = DV / L

comme les conducteurs sont de même longueur, le rapport du module des champs est le même que le rapport des différences de potentiel.

E_cu/E_al = DV_cu/DV_al = 0,61

(e) La vitesse de dérive des électrons à l'intérieur d'un conducteur s'exprime en fonction du courant, de l'aire de sa section transversale, de la charge élémentaire e et du nombre d'électrons de conduction par unité de volume n.

v = I / n A e

Dans l'équation précédente, I , A et e sont les mêmes pour les deux conducteurs. Le rapport des vitesses de dérive est donc donné par

v_cu/v_al = n_al/n_cu 

Le nombre d'électrons de conduction par unité de volume s'exprime en fonction de la masse volumique du conducteur m_v , du nombre d'Avogrado N_A et de la masse molaire M.

n = m_v N_A / M

La masse molaire du cuivre est de 63 g/mole et celle de l'aluminium est de 27 g/mole. La masse volumique du cuivre étant 3,3 fois plus grande que celle de l'aluminium le rapport des vitesses de dérive est donc

v_cu / v_al = (1 / 3,3) (27/ 63) = 0,71