Le potentiel électrique total est nul à deux endroits
sur l'axe x ainsi qu'à deux endroits sur l'axe y

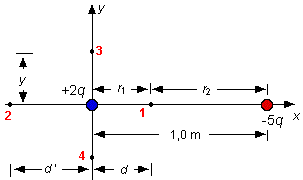
(a) L'expression donnant le potentiel électrique total est

V_tot = V₁ + V₂ = kQ₁/r₁ + kQ₂/r₂

Puisque Q₁ = 2q et Q₂ = -5q la condition nécessaire pour que le potentiel total soit nul est donc

k2q/r₁ - k5q/r₂ = 0

(1) r₂ = 2,5r₁

Point 1
Entre les charges, cette condition s'exprime en fonction de la distance d (voir schéma) de la façon suivante

(1 - d ) = 2,5d

Ce qui donne d = 28,6 cm

Point 2
À la gauche de la charge 2q, la condition s'exprime en fonction de la distance d ' de la façon suivante

(1+ d ' ) = 2,5d '

Ce qui donne d ' = 66,7 cm

Points 3 et 4
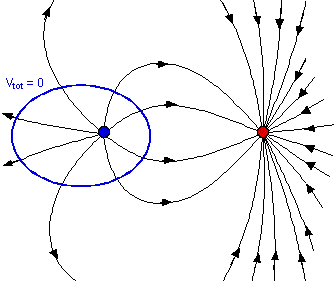
Sur l'axe y, la condition s'exprime de la façon suivante

(1 + y² )^1/2 = 2,5y

5,25 y²  = 1

Ce qui donne y = ± 43,6 cm

(b) Ces quatre points se trouvent sur la même surface équipotentielle. La figure suivante donne l'allure générale de cette surface (dans le plan de l'écran).

L'équipotentielle de potentiel nulle (en bleu)

(c) Le champ électrique varie en module et en orientation sur cette équipotentielle. Au point 1 il est orienté vers la droite et a un module égal à 34,3kq (en N/C). Au point 2, le champ électrique résultant est de 2,7kq (en N/C) vers la gauche.