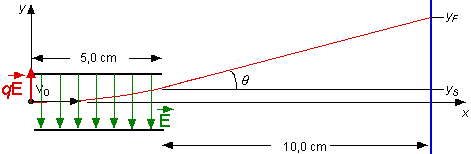
| Solution
ES2.3
(a) L'accélération de l'électron doit être dirigée verticalement vers le haut, le champ électrique doit donc être orienté verticalement vers le bas (car la charge de l'électron est négative q = - e). En négligeant l'effet du champ gravitationnel, l'accélération de l'électron s'obtient en appliquant la deuxième loi de Newton. SFy = Fél = eE = may Dans l'équation précédente, ainsi que dans les équations qui suivent, E représente le module du champ électrique. L'expression de l'accélération de l'électron est donc donnée par ay = eE /m La coordonnée verticale de la position de l'électron en fonction du temps est donnée par (1) y = yo + vyo t + 1/2 ay t2 = (eE /2m)t2 Car (vyo = 0 et yo = 0) La coordonnée horizontale de la position de l'électron en fonction du temps est donnée par (2) x = xo + vxo= vot Car (vxo = vo et xo = 0) Dans l'équation précédente vo = 150 km/s. À la sortie des plaques l'électron occupe la coordonnée de position ys, le temps que prend ce dernier pour parcourir 5,0 cm est donné par l'équation (2). La coordonnées ys est donc (3) ys = (eE /2m)(0,05/vo)2 La vitesse de l'électron à la sortie des plaques fait maintenant un angle q par rapport à l'axe x. Cet angle est donné par (4) tanq = vy/vo On peut trouver la composante vy à l'aide de l'équation (5) vy = vyo + ay t = (eE/m)(0,05/vo) À partir du schéma on peut voir que (6) yF = ys + 0,1 tan q En plaçant l'équation (5) dans l'équation (4) puis ce résultat ainsi que l'expression pour ys provenant de l'équation (3) dans l'équation (6) on obtient que le module du champ électrique doit être de 0,82 N/C pour que l'électron frappe l'écran à 4,0 cm du centre (e = 1,6 X 10-19 C et m = 9,11 X 10-31 kg). E = - 0,82 N/C j |