Le champ électrique total est 2Esinq

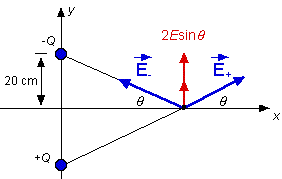
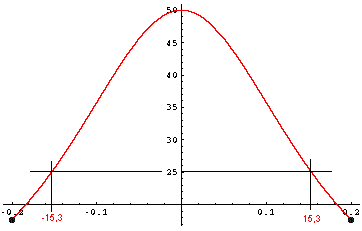
(a) Le champ électrique produit par la charge positive s'éloigne de celle-ci tandis que le champ produit par la charge négative est dirigé vers celle-ci. Le module de chacun de ces vecteurs champ est

 E₊ = E_- = E = k |Q | / (x² + 0,2²)

On peut voir sur le schéma que les composantes horizontales s'annulent pendant que les composantes verticales s'additionnent pour donner le champ électrique résultant. Le champ électrique total sera orienté verticalement vers le haut (dans le sens de l'axe y).

E_tot = 2Esinq

Puisque sinq =  0,2 / (x² + 0,2²)² , l'expression du champ électrique total est donc

(1) E_tot = 0,4 k |Q | / (x² + 0,2²)^3/2

(b)La valeur maximale du champ est obtenue lorsque x = 0. On obtient alors

E_max = 50 k |Q | (en N/C)

Nous cherchons donc la valeur de x pour laquelle le champ électrique est de 25 k |Q |. La condition mathématique à satisfaire est

25 k |Q | = 0,4 k |Q | / (x² + 0,2²)^3/2 

(2) 25 = 0,4 / (x² + 0,2²)^3/2 

En isolant x dans l'équation précédente on obtient x = ± 15,3 cm

On peut vérifier graphiquement cette solution :

Graphique de la fonction y = 0,4 / (x² + 0,2²)^3/2 
On remarque que celle-ci donne 25 lorsque  x = ± 15,3 cm