| Solution
ES1.1
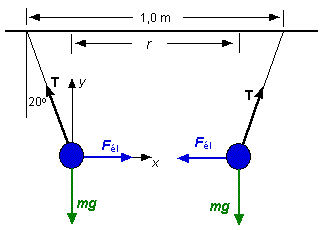
Nous savons que (1) Q1 + Q2 = 0,5 mC en trouvant le module de la force électrique, nous pouvons déterminez la valeur du produit des deux charges. En appliquant la deuxième loi de newton sur l'une ou l'autre des deux sphères SFx = Fél - Tsin20° = 0 SFy = Tcos20° - mg = 0 En éliminant T des équations précédentes on trouve que Fél = mg tan20° = 0,003567 N L'expression de la force électrique est 0,003567 = k |Q1Q2| / r2 Puisque la distance entre les deux charges est r = 1 - 2(0,6sin20°) = 0,5896 m et k = 9 X 109 N·m2/C2 , on obtient que le produit des deux charges (ce produit est négatif puisque les charges doivent être de signes contraires pour s'attirer) (2) Q1Q2 = - 1,378 X 10-13 C2 Les équations (1) et (2) contiennent les deux mêmes inconnus, Q1 et Q2 . Ces équations nous mènent à la quadratique suivante: Q12 - 0,5 X 10-6 Q1 -1,378 X 10-13 = 0 Les racines sont: Q1 = - 0,198 mC (donc Q2 = 0,698 mC) et Q1 = 0,698 mC (Q2 = - 0,198 mC) Les deux solutions sont valables. |