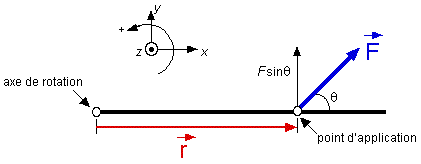
Le moment de force

Le moment d'une force, c'est sa tendance à faire tourner. Pour faire tourner un corps rigide autour d'un axe fixe, il faut que soit appliquée une force exerçant un moment de force t (tau) par rapport à cet axe.

Pour qu'une force crée une tendance à faire tourner, elle doit être appliquée à une certaine distance de l'axe de rotation. Le vecteur r relie l'axe de rotation au point d'application de la force. De plus, la force appliquée doit avoir une composante perpendiculaire au vecteur r car il n'y a que cette composante qui contribue au moment de la force. L'équation du moment de force est donc

| t_z | = r F sinq

Remarquez que l'angle q est l'angle entre les vecteurs r et F. Lorsque la rotation s'effectue dans le plan xy, le moment de force est considéré perpendiculaire au plan de rotation. Selon la règle de la main droite (ou règle de la vis droite), le moment de force est considéré positif selon l'axe z si la rotation se fait dans le sens antihoraire.

La règle de la main droite 
(montrant le sens positif du moment de force)

Lorsque plusieurs moments de force sont appliquées sur un corps rigide, il faut déterminer le moment de force résultant. L'équation suivante est la plus fondamentale de la dynamique de rotation. Tout comme la deuxième loi de Newton en dynamique de translation, elle établit le lien entre le moment de force résultant, l'accélération angulaire et le moment d'inertie du corps rigide.

S t_z = I a_z

Le principe de conservation du moment cinétique

Le moment cinétique L est à la rotation ce que la quantité de mouvement est à la translation. 

L_z = I w_z

En l'absence de moments de force extérieurs, un système ayant des composantes en rotation conservera son moment cinétique totale.

L_ztot = L'_ztot