Solution E3 chapitre 10
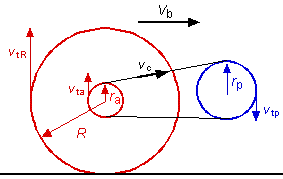
(a) La vitesse de la bicyclette s'exprime en fonction de la vitesse angulaire de la roue arrière et du rayon de celle-ci. Elle correspond à la vitesse du centre de masse de la roue arrière. Cette vitesse est de même module que la composante tangentielle v tR de la vitesse d'un point situé à l'extrême gauche de la roue arrière. (1) v b = v tR = wR R La vitesse du pédalier étant connue, il faut trouver le rapport entre la vitesse de rotation de la roue arrière et celle du pédalier. Il est important de savoir que le pignon arrière a la même vitesse de rotation que la roue arrière. La vitesse tangentielle d'un maillon de la chaîne reliant le pédalier au pignon de la roue arrière doit être la même à l'extrémité du pédalier que sur le pignon de la roue arrière. v tp = v ta (2) wp rp = wR r a L'équation précédente nous permet d'établir le rapport entre les vitesses de rotation du pédalier et du pignon arrière (ou la roue arrière). En combinant les équations (1) et (2) on obtient (3) vb = wp (rp / ra)R (b) (c) et (d) Comme on connaît la vitesse finale de la bicyclette ainsi que le temps nécessaire pour l'atteindre, il est possible de calculer l'accélération de celle-ci (0,694 m/s2). Après 10 s, la vitesse de la bicyclette est donc de 6,94 m/s. Avec les équations de la cinématique de translation (chapitre 3) il est possible de trouver la distance parcourue. Avec l'équation (3) il est possible de trouver la vitesse angulaire du pédalier ainsi que son accélération angulaire. |