• Déterminez le sens de l'accélération pour chacune des masses. Dans certaines situations, le sens de l'accélération d'une masse est évident, dans d'autres il convient de poser une hypothèse cohérente (le sens donné à l'accélération d'une masse dépend du sens donné à l'autre). Dans cet exemple la grandeur de l'accélération est la même pour chacune des masses.

• Isolez les masses. Considérez toutes les forces agissant sur chacune des composantes du système. Dans cet exemple le frottement est considéré négligeable entre le bloc de masse M et la surface du plan incliné.

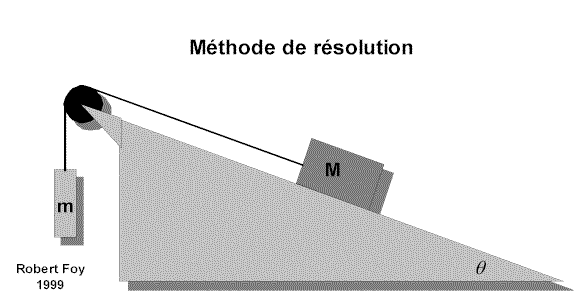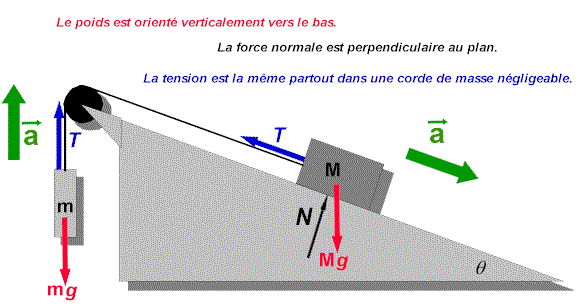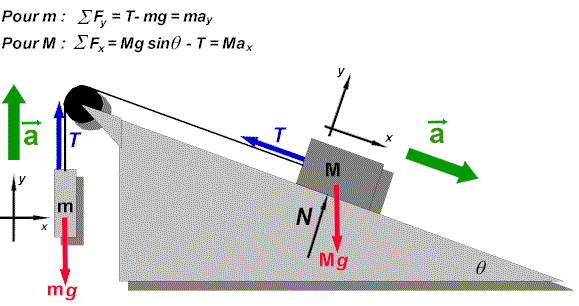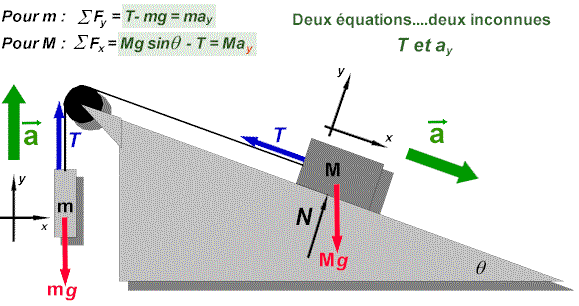
• Utilisez un système d'axes afin de déterminer les caractéristiques de la force résultante sur chacune des masses. Il est utile de placer un des axes dans le sens de l'accélération prévue. Chaque masse peut posséder son propre système d'axes.

• Appliquez la deuxième loi de Newton suivant les axes pour chacune des masses. Remarquez que dans notre exemple la tension dans la corde est la même sur chacune des masses (nous utilisons donc le même symbole).

• Les équations ainsi obtenues devraient constituer un système d'équations comportant un
  nombre de variables inconnues égal au nombre d'équations.

Les différentes étapes, proposées dans cet exemple, sont valables dans un grand nombre de situations. Les modalités d'application peuvent varier légèrement d'une situation à l'autre.

Question :
Si m = 2 kg et M = 4 kg, pour quel angle q  le
système est-il en équilibre ?

Réponse : 30^o