|
|
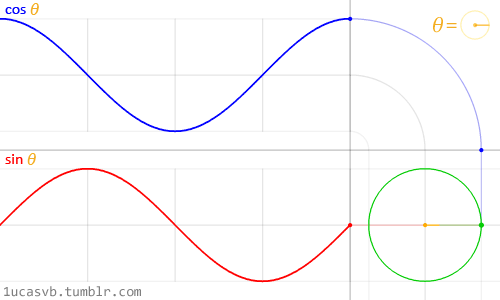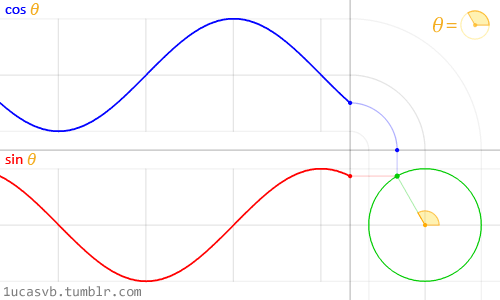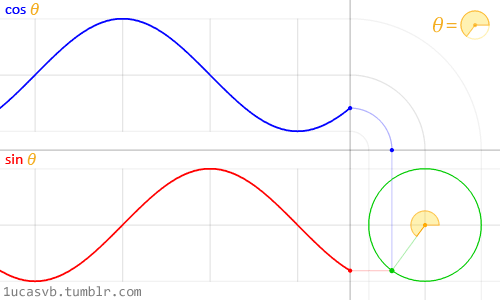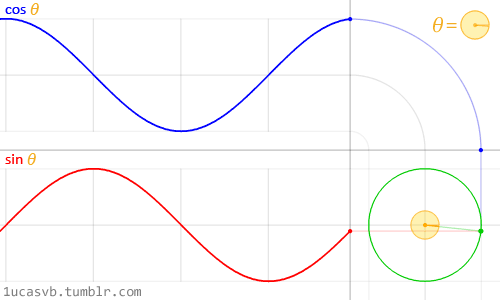
Représentation de l'équivalence entre un
mouvement d'oscillation et un mouvement de rotation. Une courbe
sinusoïdale équivaut à la courbe de hauteur par rapport au temps
d'un point se déplaçant à vitesse constante sur un cercle; une
courbe de cosinus équivaut à sa position horizontale par rapport au
temps.
Le
long d'un cycle d'une courbe sinusoïdale, on peut donc graduer et
exprimer la progression dumouvement par des angles allant de 0
à 2π radians (appelons cet angle « angle de cycle »).
Toute valeur d'angle désigne donc un moment
particulier dans la progression du mouvement ou la portion de cycle
complétée. |
 |
|
|
La constante de phase
f d'un mouvement
harmonique
Lorsqu'une oscillation ne débute pas son cycle de cosinus (ou sinus)
à t = 0, on perçoit un décalage de la courbe le long de l'axe
horizontal (axe du temps) par rapport à une courbe de cosinus. On
peut interpréter ce décalage comme un déplacement de l'axe vertical
(dans le temps)
par rapport au cycle.
Pour
une constante de phase non nulle, le sommet normalement à l'origine
(t = 0) se retrouvera plutôt à l'instant égal à « ‒f/ω ».
La position à t = 0 (l'ordonnée à l'origine) sera modifié
et sera donnée par x = Acosf.
Tout
point de la courbe régulière sera décalé sur l'axe horizontal d'une
durée f/ω,
dans un sens défini par la constante de phase. Dans l'illustration
ci-contre, une constante de phase positive a déplacé vers la droite
l'axe vertical. |

|
|
|
La phase F d'un mouvement
harmonique.
La phase du mouvement est l'état
d’avancement d’un oscillateur dans l’évolution d’un cycle normal (de cosinus).
Durant un cycle complet,
la phase avance de 2π radians. Si on considère un mouvement
décrit par une courbe de cosinus, alors un début de cycle se trouve
à un sommet de la courbe. La phase progresse donc de façon régulière
de 0 rad à 2π rad, à mesure que le temps passe de 0 à T.
Puisque « F = ωt »,
la phase permet d'exprimer où est rendu le mouvement dans la
progression d'un cycle sans tenir compte des valeurs distinctes de
t et de f,
si elles sont inconnues ou non importantes. Par exemple, pour une
situation où on ignore l'instant du départ d'un chronomètre mais
pour le quel on analyse une position donnée, il est impossible
d'identifier la constante de phase correspondante. Une infinité de
combinaisons f-t
existent, et il est possible de traiter la situation en utilisant
F
plutôt que t et f.
La valeur de la phase
n'est pas limitée à 2π rad. Ainsi, durant un cycle et
demi, la phase progresse de 3π rad, et ainsi de suite. |

|