 |
|
Introduction au
produit vectoriel
|
|
|
Le produit vectoriel est une opération entre deux vecteurs dont
le résultat est également un vecteur (contrairement au produit
scalaire de deux vecteurs qui donne un scalaire, une valeur unique
avec des unités).
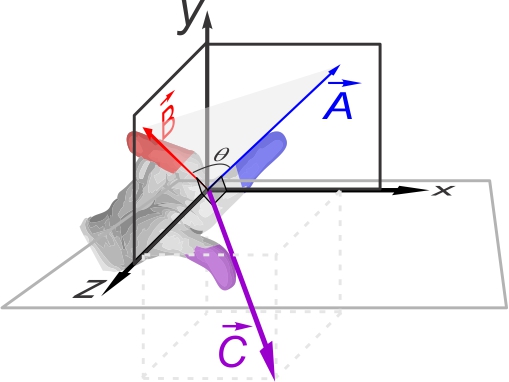
Supposons deux vecteurs
 et et
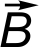 dans des
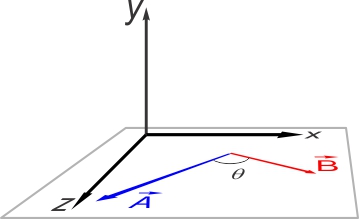
orientations quelconques et faisant entre eux un angle θ
(figure ci-contre). dans des
orientations quelconques et faisant entre eux un angle θ
(figure ci-contre).
On note
«  × × 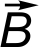 »
le produit vectoriel de »
le produit vectoriel de
 et et
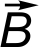 . .
|
|
|
|
|
Le résultat du produit vectoriel de
 et et
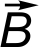 est un
vecteur perpendiculaire à la fois à est un
vecteur perpendiculaire à la fois à
 et
à et
à
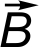 et
obéissant à la règle de la main droite. Disons et
obéissant à la règle de la main droite. Disons
 : :
 × × 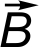 = = 
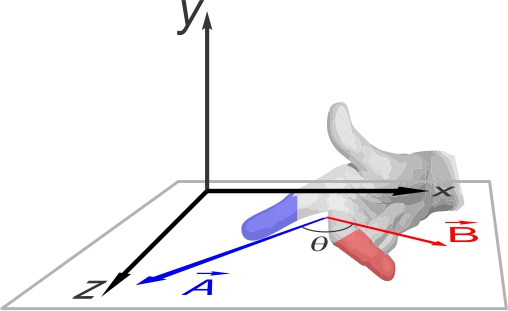
- On place l'index ou les doigts de la main ouverte dans la
direction du premier vecteur multiplié (ici
 ); );
- En gardant les doigts dans cette direction, on tourne la main de manière à pouvoir de fermer les doigts
(ou le majeur) dans la direction du second vecteur
multiplié
(ici
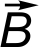 )
(du côté où l'angle est inférieur à 180°); )
(du côté où l'angle est inférieur à 180°);
- En sortant le pouce, on trouve l'orientation du vecteur qui
résulte du produit vectoriel. Cette orientation doit être
perpendiculaire aux deux vecteurs multipliés.
|
 |
|
|
|
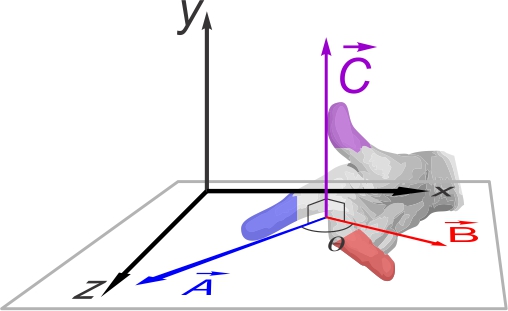
En l'occurrence, sur l'illustrtation ci-contre, le pouce pointe
dans
la direction de l'axe y postitif. Le vecteur résultant,
 , est
donc dirigé vers y+ (voir figure ci-contre). , est
donc dirigé vers y+ (voir figure ci-contre).
Lorsque l'orientation du vecteur résultant est parallèle à l'un
des axes, il est facile de déterminer le vecteur résultat en calculant seulement
le module. Le module de
 , ici,
serait donné par: , ici,
serait donné par:
C = A × B × sin θAB
Après avoir identifié la direction du vecteur (par la règle de la
main droite), on peut exprimer le vecteur résultant.
|
 |
|
|
|
Si les orientations des vecteurs multipliés sont quelconques, on
doit procéder par calcul. Les trois composantes du vecteur résultant
sont obtenues par des calculs impliquant les composantes des deux
vecteurs multipliés :
 × × 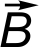 = (AyBz ‑ AzBy) = (AyBz ‑ AzBy)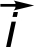 ‑ (AxBz ‑ AzBx) ‑ (AxBz ‑ AzBx)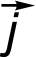 + (AxBy ‑ AyBx) + (AxBy ‑ AyBx)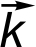
Donc :
Cx = (AyBz ‑ AzBy)
Cy = (AxBz ‑ AzBx)
Cz = (AxBy ‑ AyBx)
L'orientation du vecteur résultant est alors quelconque et peut être
difficile à illustrer clairement, mais ses composantes sont
exactement connues. Si on appelle  le
résultat de ce produit vectoriel, le module de ce vecteur serait : le
résultat de ce produit vectoriel, le module de ce vecteur serait :
C = 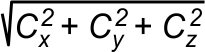
|
 |
|
|
|
|
|

|