|
Chapitre 4 : Figures et liens
utiles pour la compréhension de la matière
|
|
|
Diverses valeurs de champ électrique dans différents domaines
(cliquer pour agrandir)
L'intensité des
champs électriques observables dans différents contexte varie
beaucoup.
|

|
|
|
|
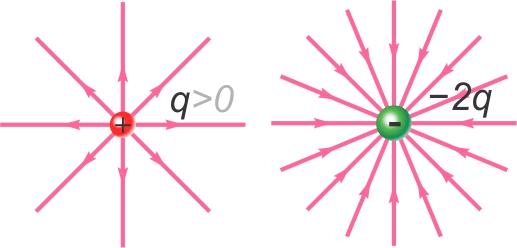
Les propriétés des lignes de champ
- Sont en nombres proportionnels aux valeurs des charges;
- Sont émises
par des charges positives
et vont vers des
charges négatives ou l'infini,
OU
Sont absorbées
par des charges négatives
et proviennent de
charges positives ou l'infini;
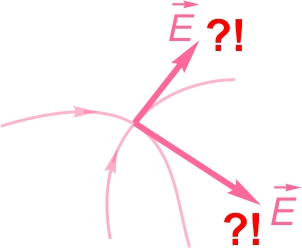
- Sont tangentes au vecteur champ en tout point;
- Ne se croisent jamais;
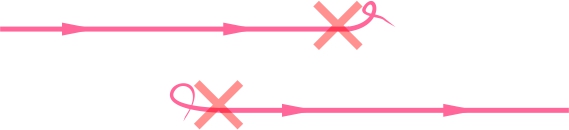
- N'émergent
jamais du le néant,
ET
N'aboutissent
jamais dans le néant;
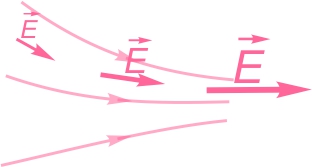
- Sont d'autant plus rapprochées que le champ est fort.
|


|
|
|
|
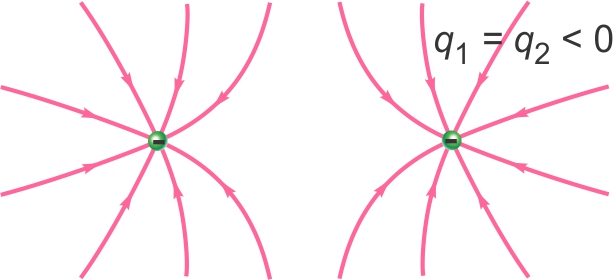
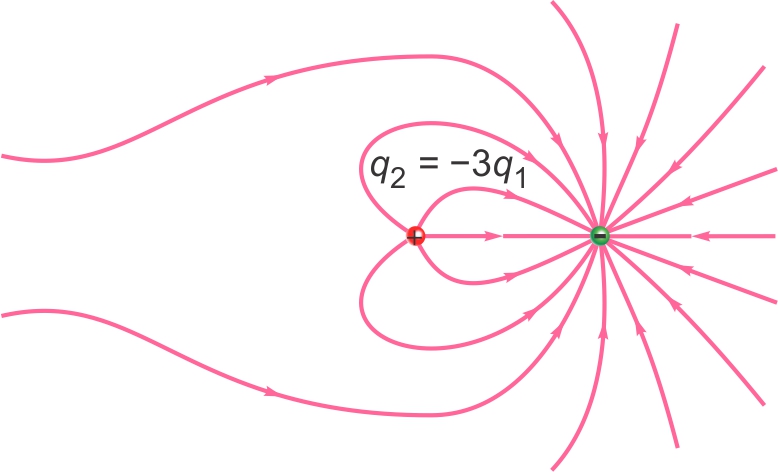
Exemples de lignes de champ
Deux charges identiques (mêmes signes mêmes valeurs)
Deux charges de signes opposés telles que q2 = −3q1
|
|
|
|
|
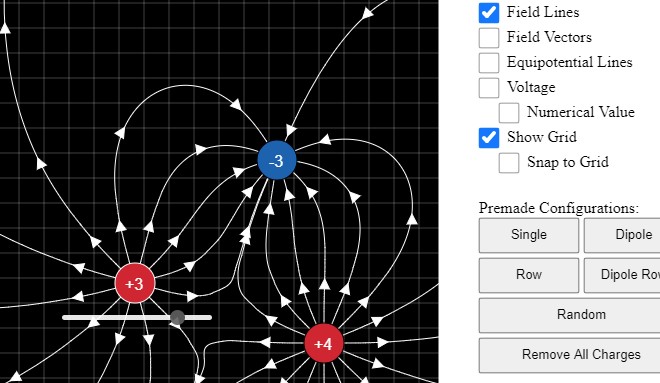
Simulateur de champ électrique produit par deux charges
Une
application en ligne illustre les lignes de
champ produites par deux charges distinctes.
Vous pouvez contrôler la valeur des charges (rapports disponibles
|q2/qsph| ≤ 5)
ainsi que leurs positions pour observer la trajectoire des lignes de
champ qu'elles produiront.
(L'application semble fonctionner sur tous les appareils, mais
déplacer les charges ne semble possible que sur certains appareils.)
|
 |
|
|
|
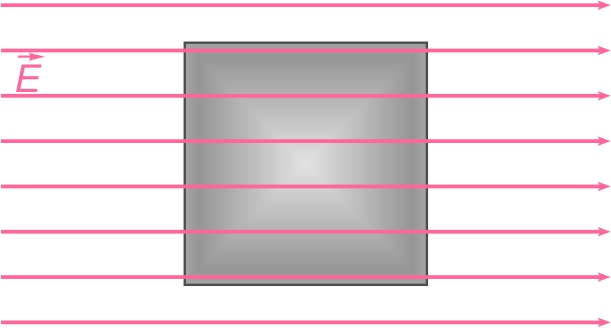
Comportement d'un corps
conducteur soumis à un champ électrique extérieur
Soit un corps conducteur placé dans un champ électrique.
Supposons a priori que le champ électrique pénètre dans le
conducteur...
|
 |
|
|
|
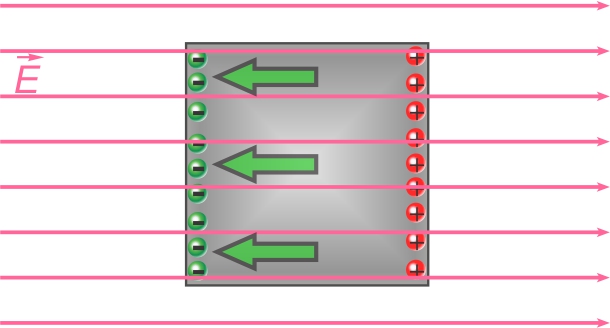
On observe une séparation de charge: certains électrons du
matériau conducteur se déplaceront sous l'effet du champ électrique
et s'accumulent sur la face exposée au champ.
Les « trous » positifs (atomes ionisés positivement) s'accumulent
sur la face opposée du conducteur, comme si des protons se
déplaçaient aussi dans la direction du champ électrique.
|
 |
|
|
|
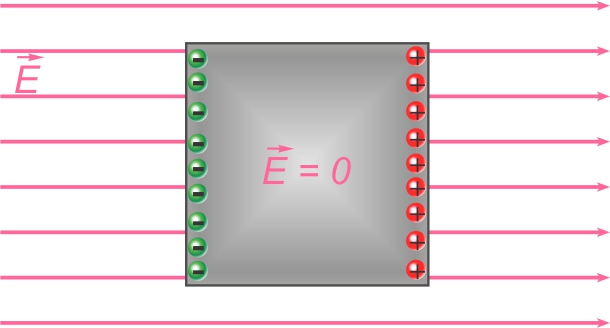
La séparation de charge génère en retour un champ électrique
interne opposé au champ externe ayant pénétré le conducteur.
|
 |
|
|
|
La séparation de charge fait précisément en sorte que le champ
extérieur est annulé par le champ interne, à l'intérieur du volume
du conducteur. Le
résultat est le même que si le champ électrique ne
pénètrait pas dans le conducteur.
|
 |
|
|
|
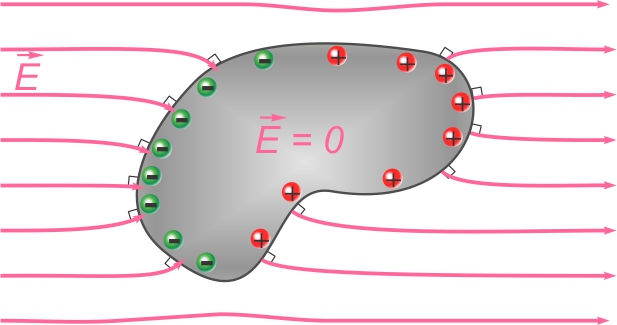
Si le corps conducteur est de forme quelconque, le champ demeure
nul à l'intérieur mais la séparation de charge peut être
irrégulière.
Les lignes de champs seront perpendiculaire à la surface partout
où elles rejoignent le corps.
|
 |
|
|
|
Effet du champ électrique
entre des surfaces conductrices rapprochées
(cas simple d'une symétrie sphérique)
|
| |
|
|
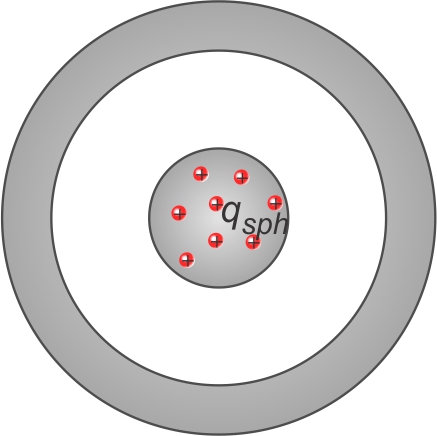
Soit une sphère conductrice chargée positivement (charge qsph) et placée au
centre d'une coquille conductrice non chargée...
|
 |
|
|
|
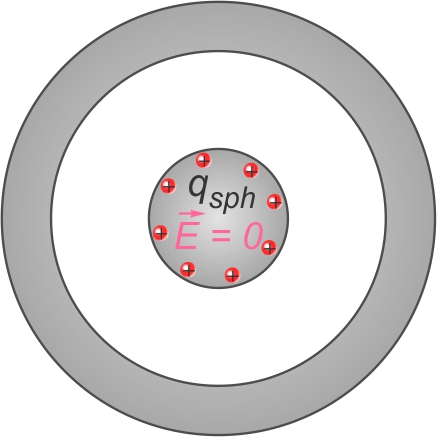
En accord avec le comportement des charges dans un corps
conducteur (électrostatique, chapitre 1), la sphère chargée verra sa
charge répartie entièrement en surface.
Aussi, le champ électrique à l'intérieur de la sphère conductrice
est nul.
|
 |
|
|
|
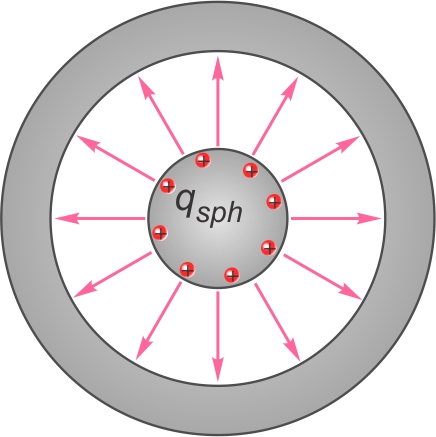
La charge positive en surface de la sphère centrale génère autour
d'elle un champ électrique dirigé vers l'extérieur (les lignes de
champ sont émises par les charges positives).
|
 |
|
|
|
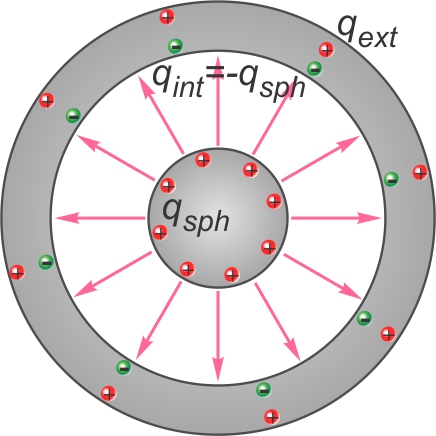
Ce champ induit sur la face intérieure de la coquille une charge
opposée (négative, ici) de même grandeur que qsph, donc
‑qsph.
La coquille étant neutre, si une charge négative couvre la face
intérieure (qint), une charge positive devra couvrir la face extérieure
(qext).
La
charge totale devant être constante (et nulle dans cet exemple) :
qint + qext = 0
qext = ‑qint = ‑(‑qsph) = qsph
|
 |
|
|
|
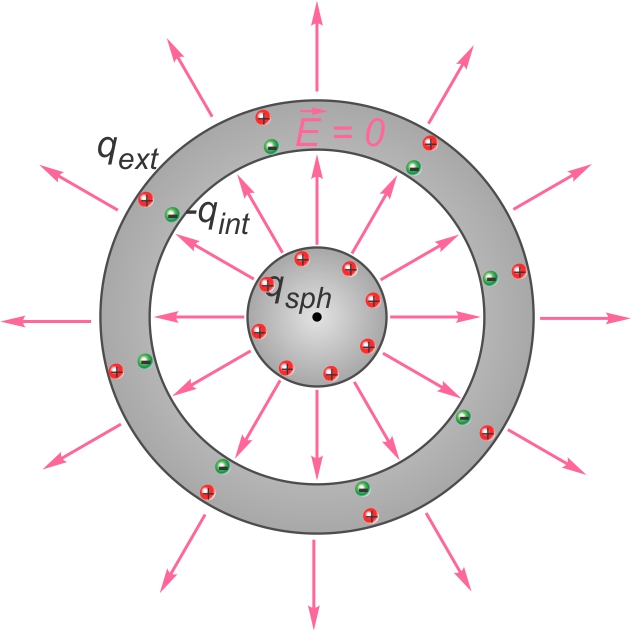
Le champ généré autour du système correspond à celui d'une charge
unique, ponctuelle, au centre du système et dont la valeur serait celle de la surface
extérieure exposée au point où on s'intéresse au champ.
Aussi, le champ à l'intérieur du matériau de la coquille conductrice
est nul (car c'est un conducteur à l'équilibre électrostatique).
|
 |
|
|
|
Dans le cas d'une symétrie sphérique, on peut calculer le champ
électrique en tout point dans l'espace autour des conducteurs. Pour
justifier l'équation utilisée, voyons d'abord des configurations
élémentaires.
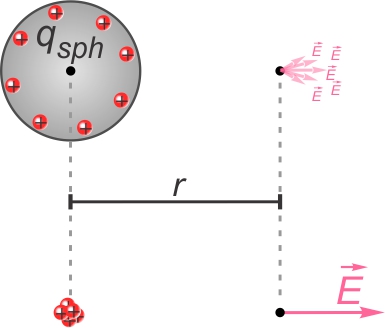
Une sphère chargée (dont la charge se répartit en surface) produit
en un point autour d'elle (à distance r de son centre) un
champ résultant généré par la sommation des champs infinitésimaux de
toutes ses charges en surface. Le champ résultant est le même que si
toute la charge était concentrée un un point en un point à la même
distance r. Ce champ est donc quantifié par la même
équation que pour une charge ponctuelle :
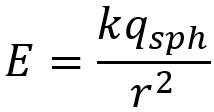
|
 |
|
|
|
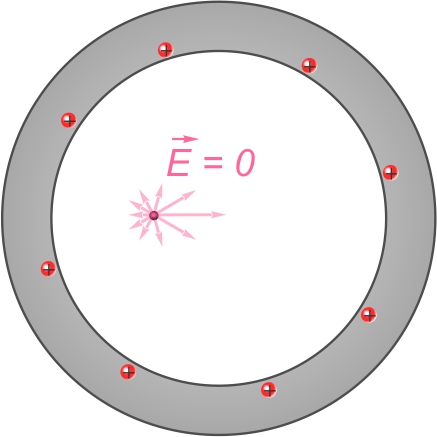
Pour un point qui serait plutôt situé à l'intérieur de la zone
creuse d'un corps conducteur, le champ est nécessairement nul. Le
calcul détaillé du champ impliquerait comme pour la sphère
précédente la sommation des champs infinitésimaux générés par toutes
les charges couvrant la surface autour du point. Mais pour toute
forme ou toute position, le champ résultant sera nul.
On peut parvenir à la même conclusion via un autre raisonnement :
aucune ligne de champ ne peut exister à l'interieur de la zone
creuse car si des charges positives sont présentes pour émettre des
lignes de champ, aucune charge positive n'est présente ailleur sur
la même surface pour absorber ces lignes. La présence de lignes de
champ entraînerait une entorse à leurs propriétés habituelles.
Conséquemment, l'absence de lignes de champ signifie l'absence de
champ électrique.
|
 |
|
|
|
Les deux principes évoqués précédemment quant à la valeur du champ
en un point autour du conducteur entraînent la conclusion suivante.
Dans le cas d'une symétrie sphérique, on peut calculer le champ
électrique en tout point dans l'espace entre la sphère centrale et
la coquille, à une distance r du centre du système : le
champ électrique est le même que celui produit par une charge
ponctuelle située à une distance r et dont la valeur est la
charge nette contenue dans un cercle de rayon r (de même
centre).
Dans la situation ci-contre, la charge nette contenue dans le cercle
de rayon rA (pointillé) est la charge qsph
de la sphère centrale :
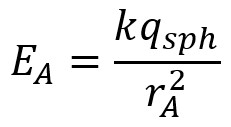
|
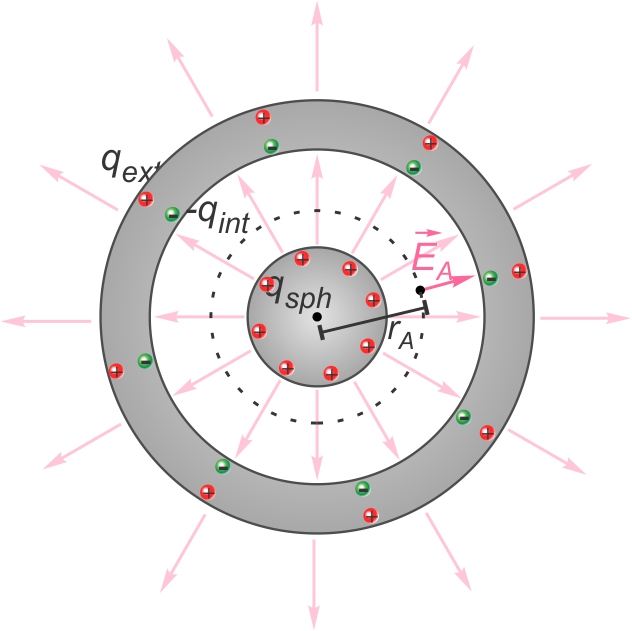 |
|
|
|
À l'extérieur du système, le champ est aussi le même que celui d'une
charge ponctuelle située au centre et dont la valeur serait celle de
la charge nette située à l'intérieur du même rayon (égale à la
charge de la surface exposée sous ce point,
qext).
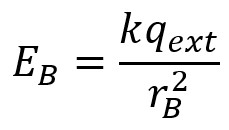
|
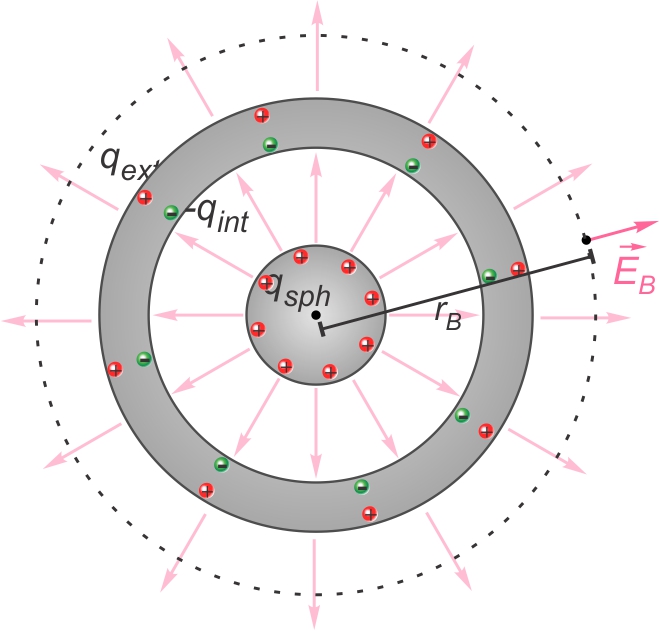 |