|
Les circuits à courant continu
|
|
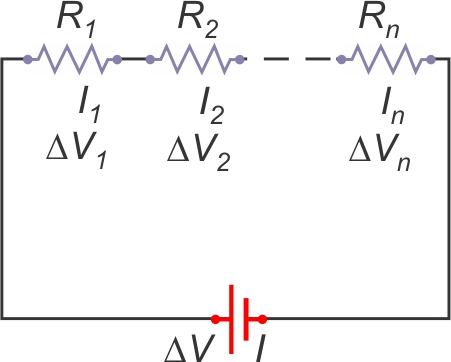
Résistances en série
Le même courant parcourt toutes les résistances :
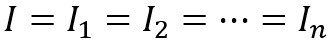
Un même courant dans des résistances différentes produit des
d.d.p. différentes;
La chute de potentiel totale ΔV est répartie en n
chutes de potentiel :
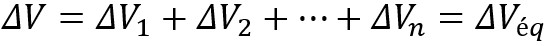
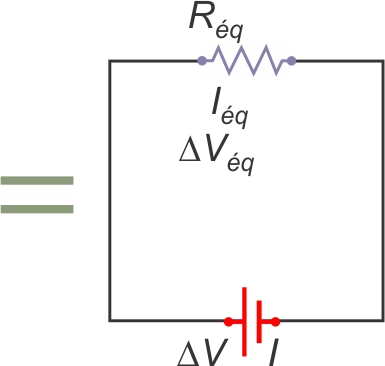
On peut remplacer l'ensemble par une résistance unique Réq qui
porterait le même courant Iéq, sous la même d.d.p. :
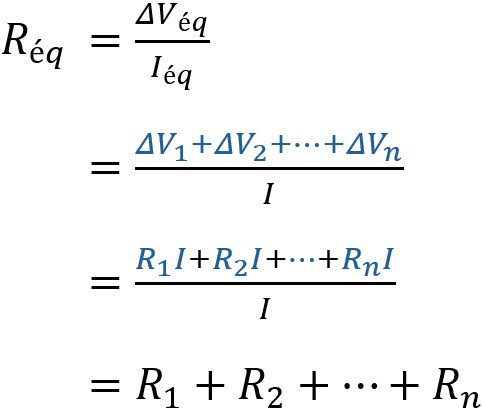
|
 |
|
|
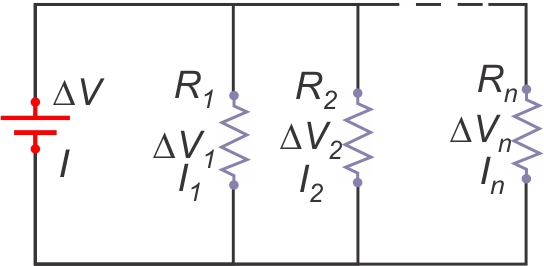
Résistances en parallèle
Toutes les résistances sont exposées au même potentiel :
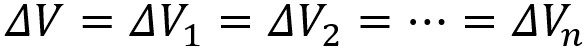
Une même d.d.p. appliquée à des résistances différentes induit
des courants différents;
Le courant total Iéq est partagé dans les n branches :
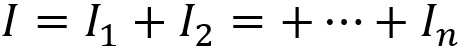
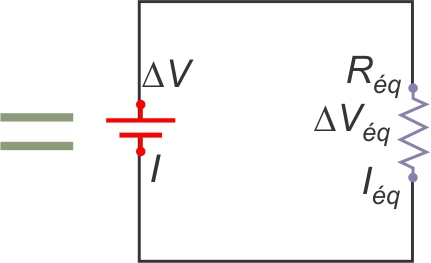
On peut remplacer l'ensemble par une résistance unique Réq qui
porterait le même courant Iéq, sous la même d.d.p. :
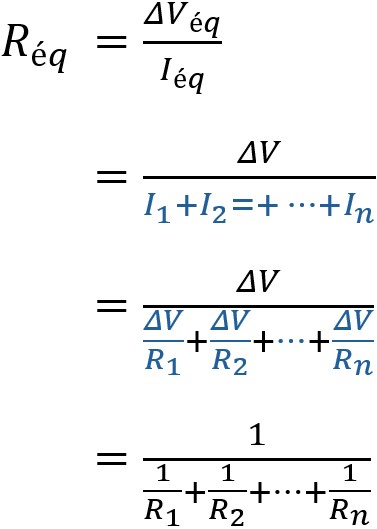
|
|
|
|
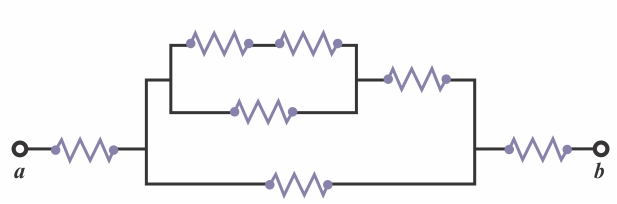
Méthode de résolution pour un circuit de résistances en
série et en parallèle
|
 |
|
LOIS DE KIRCHHOFF
Méthode
d'analyse d'un circuit à l'aide des lois
Kirchhoff
-
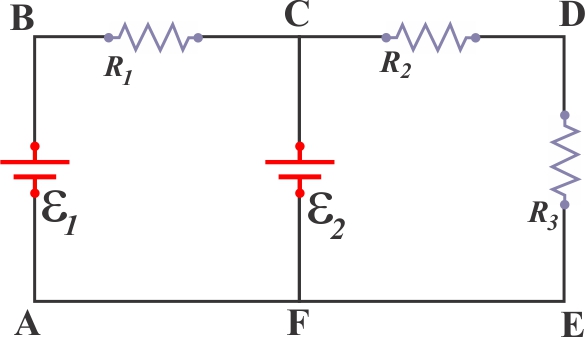
Identifier les n noeuds du circuit;
(et par utilité, quelques autres points même si ce ne sont pas
des nœuds)
|
 |
|
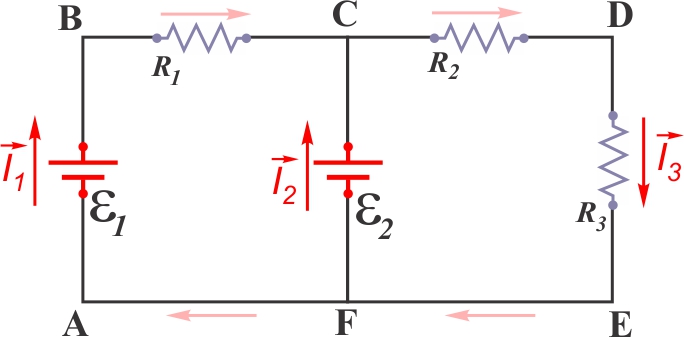
- Pour chaque branche, indiquer un sens
et un nom au courant (variables
distinctes);
- Déterminer un sens par déduction ou
par hypothèse (ce n'est pas critique: un mauvais sens
utilisé sera corrigé par des valeurs négatives après calculs);
- Pour une source, à moins de
conflit avec une autre source sur
une même branche, on peut supposer
un sens normal au courant (émis à la
borne positive).
- Hypothèse probable :
- Pour chaque source, on pose
un courant émis par la borne
positive SAUF SI deux sources
sur la même branche sont en sens
opposés.
|
|
|
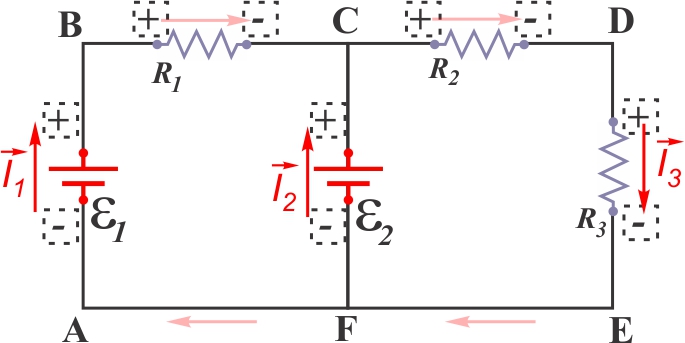
- Indiquer les polarités pour chaque composante :
- Pour une source,
le symbole définit les bornes +/−;
- Pour une résistance, le sens du courant (assumé) est le sens de la « chute de potentiel » et définit les bornes.
|
|
|
- Pour chaque maille, choisir et illustrer un sens de parcours qui servira pour appliquer la loi des mailles;
- Choisir un point de départ;
- Nommer la maille et le sens via
la suite des points rencontrés.
le sens
du parcours n'a aucun lien avec le
sens du courant, et ne peut
d'ailleurs pas le respecter partout
à la fois.
|
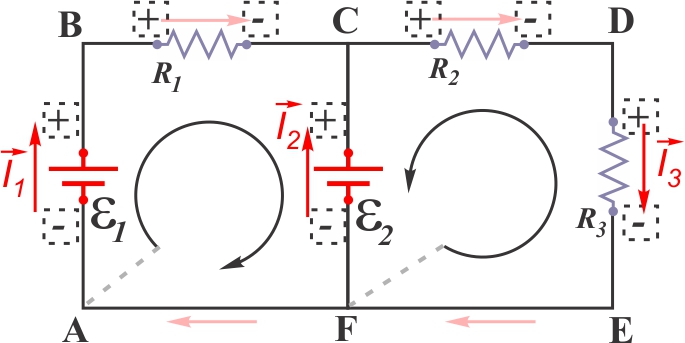 Maille
ABCFA Maille
FEDCF
Maille
ABCFA Maille
FEDCF
|
|
- Écrire la loi des mailles pour chaque maille :
- ∑ ΔV = 0
- Faire un tour complet de la maille à partir du point
de départ choisi, et
additionner/soustraire les
variations de potentiel (de grandeur
Ɛ ou RI) :
- Traverser une composante de la
borne « + » à la borne « − »
entraîne une baisse du potentiel
(−Ɛ ou
−RI);
-
Traverser une composante de la borne
« − » à la borne « + » entraîne une
hausse du potentiel.
- Vu autrement pour une
résistance :
-
Une résistance traversée dans le sens du courant entraine une chute de potentiel (ΔV = −RI);
-
Une résistance traversée dans le sens
inverse du courant entraine une hausse de potentiel (ΔV = +RI).
|
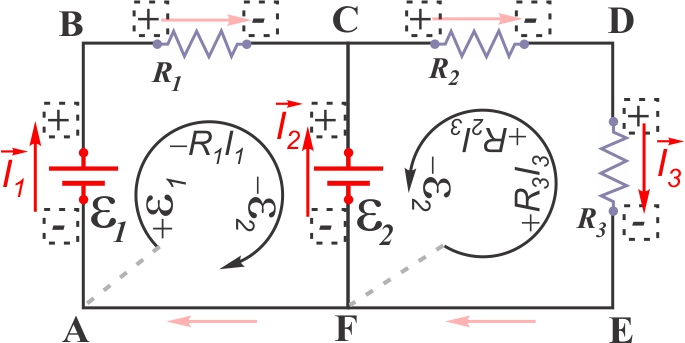 ABCFA :
∑ ΔV = 0 = +Ɛ1 −R1I1 −Ɛ2
FEDCF :
∑ ΔV = 0 = +R3I3 +R2I3 −Ɛ2
ABCFA :
∑ ΔV = 0 = +Ɛ1 −R1I1 −Ɛ2
FEDCF :
∑ ΔV = 0 = +R3I3 +R2I3 −Ɛ2
|
|
-
Écrire la loi des nœuds pour
n-1 nœuds :
(on a besoin de UNE équation de nœuds de moins qu’il y a de nœuds dans le circuit)
- ∑ I = 0
- Additionner les courants entrants,
Soustraire les courants sortants
|
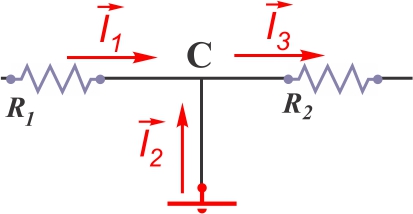 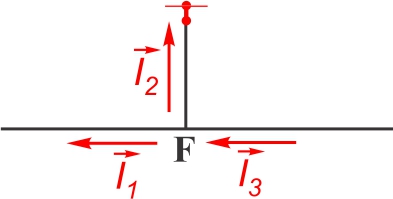
∑ IC= 0 =
+I1 +I2
−I3 OU ∑ IF= 0 =
−I1 −I2
+I3
|
|
-
Résoudre :
On a
un système de n équations et
n inconnues. On peut trouver la
valeur de chaque inconnue.
Après avoir trouvé toutes les valeurs,
on peut vérifier la validité des
résultats en vérifiant si chaque
équation de Kirchhoff donne bien zéro.
|
|
|
|
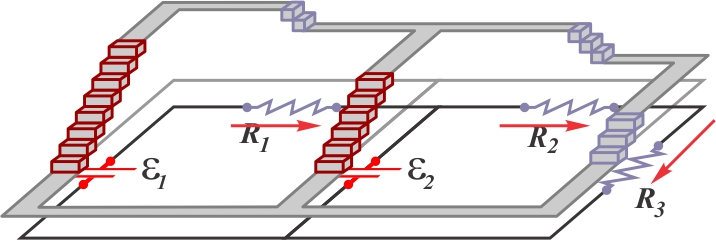
ANALOGIE entre les différences de potentiel
dans un circuit et les variations de hauteur
dans un parcours
Le même circuit peut être comparé à un
sentier comportant des escaliers.
- Les sources sont des escaliers dont
l'extrémité élevée correspond à la borne
positive.
- Les résistances sont des escaliers
qui descendent dans le sens où le
courant les parcourt.
La loi des mailles peut alors s'exprimer
au sujet de la hauteur :
La somme des variations de
hauteur pour tout parcourt fermé (revenant
au même point) est nécessairement nulle.
Remarque : le sens du courant dans les
branches de la maille ne limite pas le sens
du parcours pour appliquer la loi des
mailles; le courant pourrait être inverse au
sens de parcourt partout dasn la maille.
|
|