|
Chapitre 2 : Figures et liens
utiles pour la compréhension de la matière
|
|
|
Le classement des matériaux selon leur
résistivité
La résistivité d'un matériau varie avec la température, et le taux
de variation ρ(T) distingue en partie les conducteurs des
semi-conducteurs, supra conducteurs et isolants. |
|
|
|
|
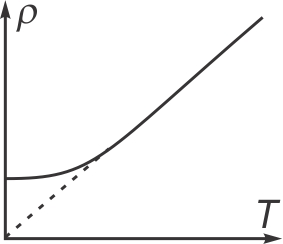
Les conducteurs
Les métaux et certains liquides Les électrons libres sont en grand
nombre dans le matériaux et tout champ électrique en vigueur dans le
matériau entraîne un déplacement des électrons dans le conducteur.
La chaleur augmente la résistivité car l'agitation thermique réduit
la facilité de déplacement des électrons libres. À faible
température, la résistivité ne devient jamais nulle en raison
d'impuretés dans le réseau d'atomes qui s'opposeront toujours au
déplacement des électrons. |
 |
|
|
|
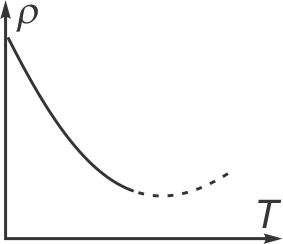
Les semi-conducteurs
Silicium, germanium,
carbone (forme diamant), et quelques dizaines d'autres matériaux Les
électrons ne sont pas libres par défaut dans le matériau. Le champ
électrique appliqué libère des électrons qui peuvent se mettre à
circuler. La chaleur facilite la création d'électrons libres
(libération par leurs atomes) et facilite la circulation du courant. |
 |
|
|
|
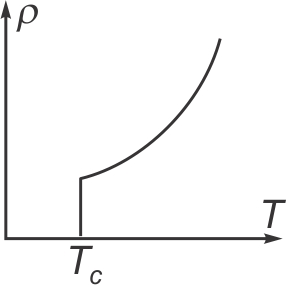
Les supraconducteurs
Certains éléments et alliages à des températures très basses
À une température « critique » très basse (entre 0 K et 200 K selon
le matériau), la résistivité chute subitement à zéro. Les
applications concrètes sont peu nombreuses en raison de la
complexité de maintenir des températures si basses, mais beaucoup de
recherche est faite sur ces matériaux, entre autres pour découvrir
des matériaux supraconducteurs à des températures moins basses. Le
matériau ayant montré de la supraconductivité à la température la
plus élevée récemment est supraconducteur à −13°C, mais à une pression
gigantesque (188 GPa). Exemples d'applications :
électroaimants des système IRM (imagerie par résonance magnétique). |
 |
|
|
|
Les isolants
Caoutchouc, verre, plastique, air/vide
Leur résistivité est si élevée qu'on les utilise comme barrière pour
le courant. Leur résistivité est très élevée mais pas infinie, donc leur
conductivité n'est pas nulle. Mais la résistivité peut être
supérieure à celle des conducteurs par un facteur de l'ordre de 1021. Le courant
est donc à toute fin pratique nulle et aucun phénomène électrique ne
peut être attribué à ce courant.
Exemples d'applications : gaines des fils électriques, supports des
lignes à haute tension. |
 |
|
|
|
Valeurs de résistivité de quelques matériaux utilisés pour leurs
propriétés électriques ... |

|
|
|
|
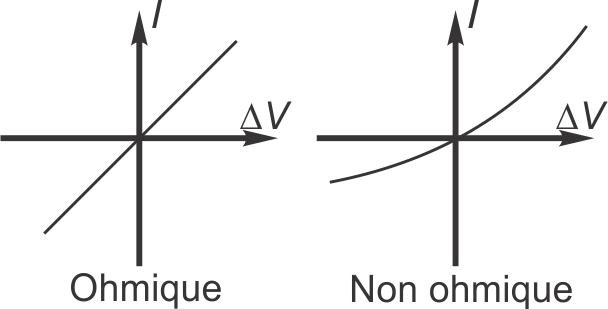
Des exceptions à
la loi d'Ohm:
matériaux non ohmiques vs ohmiques
|
 |
|
|
|
Puissance nominale et puissance
maximale d'une composante
Une résistance peut rompre si elle surchauffe. Elle a donc une « puissance maximale » (Pmax)
à ne pas dépasser, donc des valeurs limite de courant et potentiel qu’on peut lui imposer.
D’autres dispositifs sont conçus pour fonctionner à une puissance précise « puissance nominale »
(ex: ampoule de 100 W). Le fonctionnement ne sera pas optimal en dehors de cette valeur. |
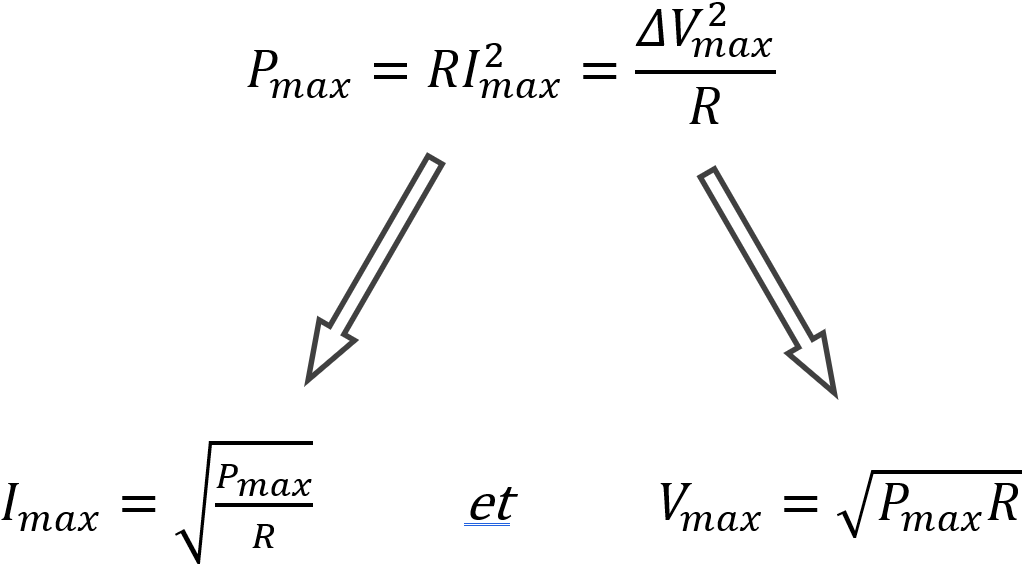 |
|
|
|
Exemple : une ampoule de 60 W (conçue pour fonctionner avec
un potentiel de 110~120 volts).
Pour une ampoule de 60 W, le
courant normal d'opération est :

Son éclairement sera vite insuffisant ou
sa longévité compromise si on s'éloigne de 60 W.
|

 |
|
|
|
Fusible (symbole : ) )
Élément conducteur conçu pour fondre rapidement (par effet Joule) et couper le courant s’il dépasse une
certaine valeur. Les éléments/appareils dans le circuit sont alors protégés des courants trop élevés. |
 |
|