|
Figures et liens
utiles pour la compréhension de la matière
Chapitre 9
|
|
|
Le
caractère vectoriel des grandeur angulaires
Toute les grandeur
angulaire peut être exprimée sous forme d'un vecteur parallèle à
l'axe de rotation et dont le sens obéit à la règle de la main droite
(pouce dans la direction du vecteur).
Par exmple,
pour un disque à plat qui tourne en sens anti-horaire (vu de haut),
si on enroule la main droite autour de l'axe dans le sens de la
rotation, le pointe vers le haut : Le vecteur vitesse anglaire
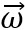 est
orienté vers le haut. est
orienté vers le haut.
Comme en translation, un vecteur accélération
angulaire dans le même sens qu'un vecteur vitesse angulaire ferait
augmenter le module de cette vitesse angulaire. |

|
|
|
|
Le roulement
et la transmission de la rotation
Si on fixe le centre
d'une roue durant sa rotation, tous les points de sa circonférence
(à une distance R du centre)
se déplacent par rapport au centre à une vitesse linéaire vR définie par :
vR = ωR
(Des points opposés de la roue se déplacent dans des
directions opposées.) |

|
|
|
|
Si la roue roule
sans glisser, le seul point de la
roue qui soit immobile est le point en contact au sol.
Dans ce cas, tous les points de la roue pivotent autour de ce point
de contact au sol.
Le centre se trouve à
une distance R du pivot, sa vitesse linéaire est donc donnée par :
vcentre = ωR
C'est la même vitesse par
rapport au sol que la vitesse d'un point du contour (dont celui au
sol) par rapport au centre.
La vitesse de l'auto est
évidemment la même que celle de l'essieu de la roue :
vvéhicule = vR = vcentre |

Donc :
La vitesse d'un véhicule
qui roule (sans glisser) est liée à la vitesse de rotation des roues
par :
vvéhicule = ωR
|
|
|
|
Transmission de la rotation
Quand les rotations de
deux disques sont liées (courroie, chaîne, engrenages, etc.), les
vitesses tangentielles des coutours sont communes :
vtA = vtB
d'où :
ωArA = ωBrB
(et αArA = αBrB)

Tous les points d'une chaîne ou courroie se déplacent
à la même vitesse autour des deux disques (ou roues dentées);
Les contour des deux roues d'engrennage se
rencontrent sans glisser ou « sauter des dents »;
Les roues d'un véhicules dont les rayons sont
différents roulent sur le sol à la même vitesse. La vitesse du sol
sous les roues est aussi la vitesse tangentielle commune des deux
roues. |

|
|
|
|
Le
moment d'inertie des solides réguliers
Les moments d'inertie
des solides réguliers les plus courants dans les exercices à faire.
Les moments d'inertie indiqués sont donnés pour l'axe
illustré dans chaque cas (un seul cas implique un axe ne passant pas
par le centre de masse).
Pour tout axe autre que celui illustré, on peut
obtenir le moment d'inertie "augmenté" à l'aide du théorème des axes
parallèles, en ajoutant au moment d'inertie (donné par rapport au
centre de masse) le produit Md², où "d" est la distance
entre l'axe réel et l'axe pour lequel ICM est
connu. |

|
|
|
|
L'énergie cinétique de rotation
Soit Ki, l'énergie cinétique de la particule
i d'un
système :
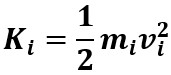
Pour un corps rigide en rotation autour d'un point O, vi est une
vitesse tangentielle :
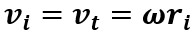
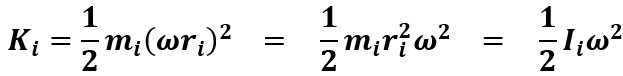
Pour l'ensemble d'un corps en rotation :
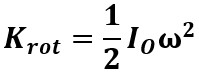
Si l'axe passe par le CM :
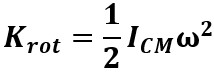
S'il se déplace en plus de tourner, Krot s'ajoute à
l'énergie cinétique de translation KO, où v est la vitesse du point
considéré comme centre de rotation (souvent le CM) :
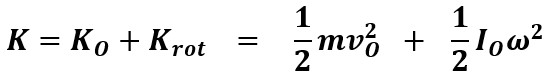
|

|
|